Ask a Geek - Quantum Mechanics 2

Okay, last geek-post for a while! Next Monday I'll talk about something else, but you're welcome to keep asking me questions about anything physics-related.

Today I'll talk about some of the most ooky-spooky aspects of quantum mechanics. If you haven't read last week's post, you probably should hit that one first, because I'll be building on those ideas here.

At the heart of quantum spookiness is the idea that before you collapse a particle's waveform, it doesn't behave like a particle. It behaves like a zillion quasi-ghostly particles located in every possible location that they can be located in.

Including, in principle, every single corner of the entire universe.

However, let me point out that the chances of a particle existing very far from where you think it's supposed to be drop off extremely sharply, so realistically, there's no chance a particle located in your left nostril will, upon having its waveform collapse, abruptly find itself on Pluto. The possibility that it could is built into our math, but that outcome is effectively impossible.

However, particles do sometimes wind up where they're not supposed to be thanks to a process called quantum tunneling.

To explain this idea, let me first give you a sketch of what the difference between an electrical insulator (like glass, wood, or helium) and an electrical conductor (called a metal) is.

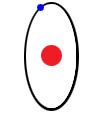
Here's a picture of an atom:


And here's a picture of a bunch of atoms:


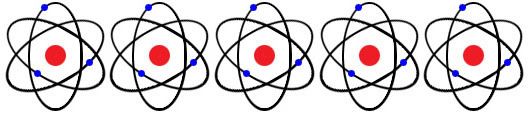
Look at the orbits that the electrons (in blue) take around the atoms' cores. Whatever this material is, it would be an electrical insulator because the electron orbits for any two adjacent atoms don't touch one another.

But here's what happens when they do touch one another:


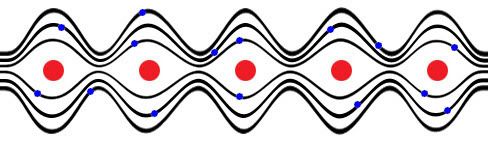
Whoa, dude--psychedelic!

See how the orbits have joined together? Now an electron can zip from one atom to the next quite easily. Electricity (which is simply a bunch of electrons in motion) flows well through this material, so we call it an electrical conductor, a.k.a. a metal.

(Just as an aside, this tendency for electrons to move easily through metals is also the reason why metals are shiny. Light is an electromagnetic wave, and it is reflected most effectively by freely-moving electrons. Hence, electrical conductors look shiny--i.e. metallic--and electrical insulators don't.)

Now, let's look at that insulator again, because it provides the perfect environment for quantum tunnelling to occur in.


The electrons attached to these atoms can also move from one atom to the next; it's just a lot harder for them.

You see, the black lines I've drawn in are just the electrons' approximate orbits. In truth, the electrons can be located anywhere within a "cloud" that centres on these lines. The chance of finding an electron way out on the edge of the "cloud" is very small--but it's not zero.

And so, every now and then, an electron will ride out to the edge of its "cloud" and hop over to the next atom. This phenomenon is called quantum tunnelling because the gap between atoms acts like a barrier, and the electrons need to burrow through it. The bigger the space, the less likely the electron will make it.

The semiconductors used to create the microchips in your computer actually rely on tunnelling. Without the freakishness of quantum mechanics, you wouldn't be on the internet right now!

But all that? That's just child's play compared to the really spooky thing that quantum mechanical particles do. What I'm about to discuss now (and it'll take a while; sorry) is sometimes called quantum teleportation.

Say you have a big hefty particle that is unstable. At some point it breaks down ("decays") into two daughter particles.


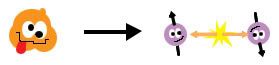
Certain quantities in nature must be "conserved", which is just a way of saying that what goes in must come out.

For example, if you have a pie and you cut it in half, all the pie is still there. The pie is conserved! If the pie had 753 blueberries in it, you will still have 753 blueberries after you cut the pie. The berries are conserved!

And, in a fundamental way, even after you eat the pie, the pie is conserved. It might be in a different form now, but all of the pie still exists in our universe.

One of the quantities that nature conserves is a weird thing called "spin". It's called "spin" because that's what it seems to be--some quantum particles behave as if they are spinning.

And I call this fact weird because some of those quantum particles--like the electron, for example--appear to be point particles. That is to say, we've tried and failed to measure the size of an electron--as far as we can tell, it is infinitely small.

And yet electrons have "spin". But if an electron has no size, what exactly is spinning?

I haven't got an answer for that and neither does anyone else. Spin is one of those properties where your instructor waves her hands vaguely and says, "It just acts like that. No one knows why...yet."

So I'll wave my hands (...these are not the droids you're looking for...) and gloss over it also. Spin just is.

Now back to quantum teleportation! When a particle with no spin decays into two particles, sometimes the two daughter particles also have no spin, and sometimes they have opposite spin.

Quick: give me a thumbs-up. (But only if you're right-handed.)


Physicists refer to spin as "spin-up" or "spin-down". This is just a reference to the way your thumb points when the fingers of your right hand are curling counter-clockwise (thumb points upward, so "spin-up") or clockwise (thumb points downward, so "spin-down".) It's a handy (har, har) way to keep track of which way the particle is spinning.

(In fact, spin can point any direction, but for simplicity, we usually pick the direction it's actually pointing in and call that either spin-up or spin-down, then measure other particles relative to it.)

If the parent particle had zero spin, and one of its daughter particles has spin-up, then the other daughter particle must have spin-down. That's the only way to "conserve" spin in this case, because the "spin-up"ness and "spin-down"ness cancel one another out--they add to zero.

But what the heck has that to do with quantum teleportation? After all, we just want to get to "Beam me up, Scotty," don't we?

Remember that the waveform of the particle doesn't collapse until you observe it. Until you take a measurement, the particle acts like a composite of a zillion different particles all behaving in their own unique way.

And a particle's spin is likewise unknown until you actually observe it. Until you've measured the spin, it doesn't point up or down--it points in all directions simultaneously.

Quantum teleportation isn't like the teleportation you see on Star Trek, but it is cool, and here's why: Imagine a parent particle decays into two daughter particles with opposite spins, and the decay happens in such a way that the two daughters shoot off in different directions.

A thousand kilometres away, you capture one of these daughter particles and measure its spin.

You have an equal chance of finding it to be spin-up or spin-down, so let's say you measure it to be spin-up this time.

But! Before you made your measurement, the spin didn't have a well-defined direction. The waveform hadn't collapsed yet, so the particle was simultaneously spin-up and spin-down.

Meanwhile, a thousand kilometres away in the other direction, someone else has just captured the other daughter particle.

Before they measure its spin, their particle acts as ours did--like a particle whose waveform has not yet been collapsed and is thus simultaneously both spin-up and spin-down.

But when that person does measure the second daughter particle's spin, they will find it to be spin-down. It must be spin-down because we found its sibling to be spin-up! Nothing else will allow spin to be conserved.

And this fact scared the crap out of physicists when it was first discovered.

You see, if the second person measures their particle's spin an instant after you measure yours, then the particles had to somehow communicate with one another faster than the speed of light allows!


Basically, this is teleportation--not of matter, but of information. Nothing in our universe is supposed to travel faster than light, and yet these two particles just coordinated their spins instantaneously over massive distances. That isn't supposed to be possible.

(Also, just so you know the lingo, the two daughter particles are said to be "entangled" when they behave like this. Physicists have done entanglement experiments, and although the "massive distances" involved are only about 30 metres, this phenomenon is verifiably real.)

Now you may be thinking, "Heeeeey now... Are you sure you physicists aren't just fooling yourselves?"

After all, I keep going on about how a particle's waveform doesn't collapse until it's observed, but how do I really know that? I'm talking about what's happening to this thing before I've looked at it.

So maybe the waveform really does have a well-defined spin and I just don't know it. That would make the instant communication of the two daughter particles an illusion. In reality, they would have organized their spin-up/spin-down positions at birth and just kept them.

In fact, this whole scenario that I've described was proposed by Einstein, Podolsky and Rosen as a way to poke holes in the idea that the waveform doesn't collapse until after it is observed. Einstein famously described this apparently instant communication as "spooky action-at-a-distance", and he considered it absurd.

Of course, being Einstein, he was predisposed toward thinking nothing could travel faster than light, wasn't he? Father of relativity and all that.

But then a fellow named Bell showed (mathematically, which means I'm just going to wave my hands and hope you believe me) that it isn't possible for there to exist some unknown mechanism to allow the two daughter particles to only seem to be in instant communication.

Bell found if you try to insert a very generic term into the equations to account for this unknown mechanism, you wind up getting an inequality. (Where an inequality is something like "1 does not equal 3"; it's pretty hard to argue with a blatant inequality.)

The orthodox view of physicists today is that quantum mechanics does allow instantaneous communication between "entangled" particles. We don't know what the mechanism for this is, but for now, that's our most conservative and logical explanation. There is always the possibility that as we learn more, we will discover a less "spooky" reason, but we aren't there yet.

The reason why entanglement is sometimes called quantum teleportation is because one elementary particle is identical to every other. There is no way to tell electrons (for example) apart.

So you can, with a bit of brain-flexing, think of ways to use entanglement to effectively move a person instantaneously across huge distances. In a practical sense, the process is impossible, but we can at least dream it, even if our understanding doesn't (currently) allow it to really happen.

The idea here is you would first entangle every particle of your body with the sister particles in a doppelganger of you that had been built far, far away. Then, you somehow observe every particle in your body.

The states of all the particles in your doppleganger would then become identical (but opposite) to yours, and since the "oppositeness" of most particles doesn't matter to biology, the doppelganger would instantly become you.

Or at least a copy of you. It's all pretty creepy, actually, but it would potentially allow humanity a way to explore space. Astronauts wouldn't so much travel as be cloned in distant locations, and then the clone could be re-cloned here on Earth to report their findings.

Which is...brrr...just not something I'd volunteer for.

~~~~~~~

As always, please feel free to ask questions or request clarifications in the comments. I'm also happy to having crazy brainstorming sessions about how you can turn these ideas into stories!

Ask a Geek - Quantum Mechanics, Part 1

Today, I'm going to talk about quantum mechanics. But first, I'm going to rant a little.

You see, I have a pet peeve about how quantum mechanics is described to laypeople and to undergraduate college and university students. I'll get to that in a moment.

First, some background:

When you're talking about extremely small things, the tiniest bits of matter act in some very odd ways. The most famous of these is that these tiny bits of matter behave like they are both a wave and a particle at the same time.

The following video does a really great job of explaining how scientists know that, but ARGH ARGH ARGH this video is in outrageous violation of my pet peeve.

So first, please watch this. Then, I'll explain why I'm unhappy with part of the video.



There! There at the end--that little eyeball on a stick? When they trotted that creature out, that's when I started getting annoyed.

You see, people who are trying to explain quantum mechanics always seem to want to play up the ooky-spooky aspect that if you observe the particle, it behaves differently. In the above video, they even state that the particle behaves "as if it were aware it is being watched."

Stop! Hammer-time! Reality check! What does it mean when you observe a table?

It means that some light hit the table, bounced off, and then your eye detected the reflected light.

What does it mean when you observe a particle?

The same damned thing. It means you bounced something off that particle.

However, while bouncing a little light off a table doesn't noticeably affect the table, if you take a teeny-tiny particle and then bounce another teeny-tiny particle off it, of course you're going to screw up what the first particle was doing! If you were shooting marbles at the double slit, but whacking each of them with a hammer as they flew past, that would affect the pattern they made, wouldn't it?

"Observing" isn't a benign activity when you're talking about objects this small. Any method you use to measure what a particle is doing will affect what the particle is doing. There is no measuring technique delicate enough to prevent that from happening.

I'm always annoyed when people play up the ooky-spooky stuff to make quantum mechanics sound all weird and cool. It is weird and cool, but there is no place for spin-doctoring in science. That amounts to perpetrating a fraud, in my opinion.

Ahem. Rant over; now I'll get on with the rest of the discussion.

The video introduces a few terms that may not be familiar to you, so I'll sketch out what they were talking about.

There was a moment when the video hurled a bunch of equations up and then blathered about the particle being a "superposition" of states. And you may be thinking, "What the heck?"

Here's what they were trying to convey: when it comes to quantum mechanics, physicists don't necessarily have a grasp on the big, fundamental "What is it?" questions, but we have an absolutely rockin' handle on the math.

Quantum mechanics is essentially a mathematical model for what reality is doing. When I say "model", that means the math is a way for humans to wrap their brains around something they can't personally see--just like a set of blueprints is a model that helps you wrap your brain around how a building was constructed.

Quantum mechanics is a reeeeeeally successful model. It can calculate and predict answers that match reality accurately to a few parts per million. I mean, it's just gorgeous--and that's part of why we believe this stuff; when something works really, really, really well, you generally know you're on the right track.

Now I have to describe what the math does without using math, so bear with me for the next little bit.

Say that you're trying to describe where a particle is going to travel to, and you want to use quantum mechanics to do it.

Your strategy would be to take all the possible paths the particle could travel along and then average them together.

This smeared-together wad of possibilities is called the particle's "waveform" (another term that got used in the video without explanation.)

Until the particle actually bonks into something (like the wall or another particle), it behaves as if it could take any--or all--of the possible paths.

In other words, that one particle acts like it is a zillion different particles all taking their own unique path through space.

And these hypothetical particles affect each other, which is why when you shoot one electron through a double slit (as portrayed in the video), you still end up with an interference pattern. As long as the particle hasn't been jostled on its way to the wall, it acts like a zillion hypothetical particles in motion toward the wall--and all those particles are interfering with each other.

However, as soon as the particle bumps something, then it chooses one path. It starts acting like one particle instead of a zillion mutually-interfering particles.


And so you stop seeing an interference pattern the moment you "observe" the particle because "observing" it means bonking it with another particle. That forces the original particle to act like a single lump of matter instead of a wave of many possibilities.

Pretty freaky stuff, hey?

This is what "collapsing the waveform" means. Before the collision, the particle acts like a composite (a "superposition") of a zillion potential behaviours. After the collision, those myriad possibilities collapse down to just one possible behaviour.

Of course, you don't know which path the particle will decide to take when you bonk it. There is still a random element. Also, if you leave the particle alone for long enough after the collision, it will "de-cohere", or begin to act like a smeared-together average of all possibilities again.

~~~~~~~

Next, I'll explain the term "quantization". When physicists say something is "quantized", that means it changes in little steps.

I'll use a rainbow as an example--think about how all the colours in a rainbow flow together.



They change from one colour to the next in a continuous way. But now consider the following rainbow:



In this image, the colours change in well-defined steps. You can put your pencil-tip down on any part of the rainbow and there is no ambiguity about what colour your pencil-tip is resting on.

In this second image, the colours are "quantized", which means that when the colour changes, it does so in a single step, not continuously.

A lot of things in quantum mechanics turn out to be quantized, but I'll just discuss one of them because I can sketch out why it's quantized fairly easily.

This is the typical drawing of an atom. In the centre is the nucleus and zipping around the outside are, in this case, three electrons.


Here, for clarity, I show the same thing with only one electron. What I want you to note is I've drawn the electron as a particle moving in an orbit around the nucleus.


But wait! Remember that particles can be thought of as waves too. This is a picture of wave. What would happen if we tried to wrap this wiggly shape around the nucleus?


My schematic below attempts to show you the answer to that question. You can see that for certain lengths of waves, the wave fits nicely around the nucleus and the "peaks" of the wave line up properly when they wrap around back to their starting position.



But it's only some wave-lengths that do this. For in-between values (like the drawing in the middle), the waves don't line up properly when they come back to the start.

And those kinds of orbits around the nucleus are not allowed; only the stable, neat-and-tidy looking orbits are.

Thus, the electron's wavelength when it is orbiting the nucleus is quantized. If you give that travelling electron a little jolt of energy, its wavelength has to change by a jump--a discrete step--in order get up to the next "allowed" configuration.

Now a big fat caveat: These "allowed" configurations are called standing waves, and the cartoon I drew above looks nothing like the three-dimensional "clouds" of probability that electrons actually form around a nucleus. You can see an example of some of the wild shapes they do form by clicking this link.

An electron zipping freely through space, not attached to any nucleus, can have any wavelength it pleases (and in fact, if its waveform hasn't been collapsed yet, it has all wavelengths simultaneously.) It's only when the electron is bound to another body that its wavelength becomes constrained--i.e. quantized.

All sorts of other physical quantities--like angular momentum, energy, and even sound vibrations--become quantized when you have more than one particle interacting with each other.

Physicists also refer to light as being quantized, meaning that there is a smallest-possible chunk of light called a photon. In fact, the term "quantized" is an all-purpose term that means anything that comes in blocks or steps, rather than changing in a smooth, continuous way.

I'll stop here, although there's much more to talk about with regard to quantum mechanics. In my next post, I'll try to discuss more of the "spooky" parts of quantum mechanics.

~~~~~~~

Have you got questions? Suggestions? Something that didn't make sense or something you'd like me to touch upon next time? Please feel free to drop me a note in the comments, and I'll do my best to either answer your question there or to incorporate it into my next Ask a Geek post.

Ask a Geek - Special Relativity, Part 2

Eek! Quick, quick--I must get in another blast of that sweet, sweet special relativity before bed.

I mentioned in my last geek-post that as a body starts moving faster (close to the speed of light), its mass increases. This is part of why humans are unlikely to ever personally experience some of the weirder effects caused by special relativity. To accelerate a body takes energy, and the amount of energy depends on the mass of the body. The larger the mass, the more energy it takes to speed it up.

And therein the problem, because if your mass increases with speed, then it takes ever more disproportionate amounts of energy to speed up even faster.


Theoretically, it would take an infinite amount of energy to speed a body with mass up to the speed of light. It takes obscene amounts of energy even to get close to that speed. With tiny particles, we can do it, but the cost of something like the Large Hadron Collider tells you it isn't easy, even then.

So how does light manage to travel at the speed of light?

First, I'll mention something that I plan to discuss more when I do my post on quantum mechanics: elementary particles can be thought of as either a wave or as a particle. In my discussion of special relativity so far, I've talked about light as a wave. Now I'll talk about it as a particle.

The smallest portion of light is a particle called a photon, and unlike many other particles we know of, the photon has no mass.

But wait--how can something with no mass even exist?

Short answer: because of an amazing loop-hole in the laws of physics.

A body with mass cannot be accelerated to the speed of light because that takes too much energy. The photon, however, has no mass so it can move at the speed of light. But something with no mass shouldn't be able to exist.

However! Remember how in the last geek-post I said that the faster you move, the more time slows down for you? What I didn't mention is that if you move at exactly the speed of light, time stops for you.

The reason the photon doesn't poof out of existence is because it doesn't experience time. It moves at the speed of light, and therefore it never ages. It can't stop existing because it can't undergo any sort of change.

You'll also remember from the last geek-post that I argued light can't appear to slow down or stop, or the changing electric and magnetic fields that create the wave would also stop and then the light would cease to exist.

Now we've got a completely different argument for that same thing. Light can't slow down or stop because if it did, then the photon would start to age and would immediately poof out of existence because it has no mass.

It's like something that isn't real but manages to exist because of a loop-hole. The universe is a strange and beautiful place, eh?
The last thing I'll talk about with regard to special relativity is the symmetry of it.

Say you're sitting on a train moving at close to the speed of light. You zip past someone who is standing still.

How is this different than if your train was standing still and the other person was the one zipping past?

The truth is that it's no different, and that leads to some mind-bending conclusions.

Remember how time slows down for a person who is moving? A person who is standing still will look at the person who is moving and think they are operating in slow motion.

However, the person who is moving will observe the rest of the universe (including the person standing still) to be moving in slow motion! The person in motion can argue that they're the one who is really standing still.

Special relativity is symmetric. If you are in motion, you will observe the world outside to be behaving as if it's in motion, not you.

This gives rise to the famous Twin Paradox. Consider what would happen if you sent one half of a set of twins (let's call her Rupinder) out on a rocket ship travelling close to the speed of light.


Rupinder's twin Mandeep is sitting on Earth. On the flight out, Mandeep will observe Rupinder to be acting and aging in slow motion. He will think he's growing older than his twin.

But Rupinder will also be observing Mandeep to be acting and aging in slow motion! She will think he is the one getting older!

There's no way for these two to tell who is in motion and who is standing still just by looking at the other twin or taking measurements. This leads to the question of who is really going to be older when Rupinder stops travelling and comes back to Earth. Thus, the "Twin Paradox".

There's actually no paradox. Mandeep is going to be older when Rupinder comes back.

You see, I haven't been very precise about stating when these odd predictions of special relativity are valid. It turns out they are only valid for people and objects travelling at constant speeds.

In order to come back to Earth, Rupinder has to decelerate, stop, then turn around and accelerate again. In other words, she has to stop moving at a constant speed.

When she does that, the universe gets a chance to bring her reality and Mandeep's reality back into sync. That happens again when Rupinder slows down and stops upon reaching Earth.

As long as she is travelling at a constant speed, then what she sees and what Mandeep sees are equivalent, and neither one of them can tell which of them is in motion and which is standing still (unless they let what the rest of the universe is doing influence their decision.) Acceleration and decelerate break that symmetry, however.

General relativity was Einstein's attempt to bring acceleration into the picture. Special relativity--which is what I've been talking about here--only applies in the special cases where acceleration doesn't occur or isn't important to the problem. Einstein came up with both theories, but general relativity is where the math really started to get ugly.

And so, that's where I'll stop talking. :-)

~~~~~~~

Again, have you any questions? Anything you would like clarified? I'd be happy to discuss this more in the comments!

Ask a Geek - Special Relativity

Today, I'll talk about special relativity, which is one of the topics of modern physics that I think most people are pretty intrigued by. It's a nice thing to discuss because a lot of its most surprising predictions can be demonstrated without math via "thought experiments".

The cool thing about this topic is everything I'm going to discuss here follows from one simple assumption: The speed of light is constant.

That is to say, everyone in our universe who measures the speed of light in a vacuum will get the same value (although Rigellans probably use different units than we do. Heck, even Americans use different units than most of us do.)

That doesn't sound too outrageous, does it? That the speed of light is constant?

But it is, and here's why: If we believe that the speed of light is the same for everyone, that necessarily means that time doesn't run at a constant rate for everyone, and that two different people can measure the length of the same object and legitimately get different answers. It also means two events that seemed simultaneous to you might have happened at different times according to someone else.

Imagine you're sitting on a train moving 75 km/hr. On the track next to yours, another train is moving at 100 km/hr. How fast does the train beside you appear to be moving relative to you?

The answer (to an excellent approximation) is: It moves at (100 - 75) = 25 km/hr relative to you.

Now imagine you're sitting on a train moving at 75% of the speed of light. You look out the window and see a beam of light travelling parallel to your train at 100% of the speed of light. How fast does the beam of light appear to be moving relative to you?

This is the shocking part: That beam of light will appear to be moving at 100% the speed of light relative to you, NOT 25% of the speed of light.

How is this possible? The answer is that because you are travelling so quickly in space, you are moving less quickly through time. In other words, when you look over at that beam of light, you're moving in slow motion and don't realize it.

Below is a pair of diagrams to help you understand how this works. For this first one, imagine that you and a buddy are drag-racing across the desert. You are both driving cars that travel at exactly 100 km/hr.

If you both cross the start line at the same moment, aim directly at the finish line, and travel at the same speed, then of course this race is going to end in a draw, right? Neither of you will be able to pull ahead of the other.

But wait--what if one of you chooses a different path through space?



As you can see, if you drive away at an angle, you will need to travel a longer distance than your friend does to cross the finish line. That means your friend is going to win the race because he's travelling more quickly forward (in what I've labelled the x-direction) than you are.

But let's re-label the dimensions on the above image and re-imagine what's happening. Now you and your friend are drag-racing through time.



This re-labelling isn't such a weird thing for me to do, because our universe has four dimensions--the three spatial dimensions (up/down, right/left, backward/forward), and time.

In my first image, your friend moved in one dimension (purely forward in the x-direction), and you moved in two dimensions (forward in the x-direction, but also sideways in the y-direction)

In this second image, your friend is still moving in one dimension--except it's time, now--and you are again moving in two dimensions (time, but also space.)

To make it clear, your friend is sitting on his couch, and that means he is only moving through time, not space. You, however, are in a rocket ship moving through space while you also move through time.

Remember how, in the first case, you were going to lose the drag race because you hared off in another direction? The same thing goes here. When you travel through space, that forces you to travel less quickly through time.

In other words, time slows down for you when you move through space.

Another way to think about it is that you are moving at the speed of light all of the time (and so is everyone else), but most of that forward motion is sending you through time rather than space. It's only when you start moving quickly through space that you stop moving quite so fast through time.

I'll pause here with the standard caveat that this time-dilation effect isn't measurable until you're moving at a noticeable percentage of the speed of light. Humans can't manage that (yet.) The speed of light is over 10 billion km/hr and our current speed record for manned flight (by Apollo 11) is just under 40,000 km/hr. Time dilation has been seen in accelerated particles, but we're not likely to ever see it happen to a human being.

Now I'll discuss why, when you're travelling at speeds close to the speed of light, time slows down for you.

First, let me explain what light is.

When you run electricity through a wire, that creates a magnetic field around the wire. Likewise, when you wave a magnet around, the motion of the magnet creates an electric field around it.

That's a pretty stripped-down explanation of what's happening, but the thing for you to take away is the idea that a changing electric field creates a (changing) magnetic field and a changing magnetic field creates an (changing) electric field.

Which, if you think about it, creates a chicken-and-egg scenario. The changing electric field creates a changing magnetic field. So wouldn't that in turn create a changing magnetic field that could create a changing electric field that could create a changing magnetic field, etc. etc. to infinity?

Yep. It does. That is what light is: a chain of electric and magnetic fields that create one another and thus zip away into space. (It's also why light is called an electromagnetic wave.)



Now let's return to one of the prior examples. Imagine sitting on a train travelling at 75% of the speed of light--in fact, let's speed up the train. Let's say it's travelling at 100% of the speed of light.

Now imagine looking out your window at a beam of light travelling alongside you. If time didn't slow down for you, what would you see?

You would see that beam of light appear to just hang there in space beside you, frozen.

And that's not possible, because only changing electric fields create magnetic fields and vice versa. If the beam of light appears to be frozen, then it has to stop existing!

To put that another way, light can't stop, or it doesn't exist. That's why you can't catch a bucket of light. When the light hits the bottom of the bucket, it either has to reflect away or be absorbed as heat energy. Light can't sit still.

Thus, to be internally consistent, our universe doesn't allow light to even appear to stop. If we speed up (trying to see light appear to stop), then time slows down for us in such a way that we only see light moving at the same speed it always appears to.

The obvious question is why? Why does our universe have a speed limit? Why does it enforce it in this way, by not allowing us to even see light appear to slow down or stop?

That's a big hairy question, and right now, science doesn't have an answer for it. All we can say is that it is this way, and that the rules are internally consistent for a wide range of phenomenon.

After all, special relativity doesn't just predict that time slows down when you're travelling quickly. It also predicts that objects get shorter in the direction they're travelling and that the object's mass increases. Those are pretty weird, anti-intuitive facts, but again, all these predictions bloom out of that one very simple statement:

The speed of light is always constant. For everyone--no matter how fast or slow they are travelling relative to light.

Now, I've been trying like a mofo to think of some way to explain how the length of a fast-moving object gets shorter without resorting to mathematics, and I even dragged my husband (the black hole guru) into the discussion, but the short answer is we don't know of a way.

I've got a mathematically simple way to demonstrate that a stationary person will measure the length of a fast-moving object to be shorter than a person riding along with that object will. Unfortunately, it's still math, so I've elected to skip it.

Instead I'll show you something that's arguably weirder: simultaneous events aren't simultaneous for everyone.

Here's what I mean by that. Imagine a train car moving at close to the speed of light. It has a light bulb suspended in its centre. At a certain point in time, a person travelling on the train turns on the light.According to the person on the train, the light from the bulb spreads out at a constant speed in all directions. The leading edge of that light thus forms an ever-increasing sphere centred on the bulb.

Because the bulb was in the middle of the train car, the light then strikes the front and the rear walls of the train car at the same time. You can see that in the diagram above.

Here's where it gets odd. Imagine someone standing by the side of the train track watching this happen through the window. Because the speed of light is also constant for this stationary person, they too see the light spreading out at a constant speed in all directions from the bulb's initial position. The light still forms a spherical shape.

However, while the light is spreading, the train car is moving forward.According to the stationary person, the light strikes the rear wall of the train car first and the front wall of the car second. In effect, the rear wall of the train car "caught up" to the light while the front wall is "fleeing" the light and thus takes longer to be struck by it.

This is something only relativity gives us. The moving person saw the light strike both walls simultaneously, but the stationary person saw the same light not striking the walls simultaneously. And both people are correct about what they saw!

I'm going to stop there because this post is already massive, but I'll try to post something tomorrow about the symmetries of special relativity--which includes the famous Twin Paradox.

~~~~~~~

Questions? Need clarification on anything? Got a suggestion for something else I could talk about with regard to this subject? Please feel free to drop me a line in the comments!